(1)從單一測站之紀錄決定震央位置:

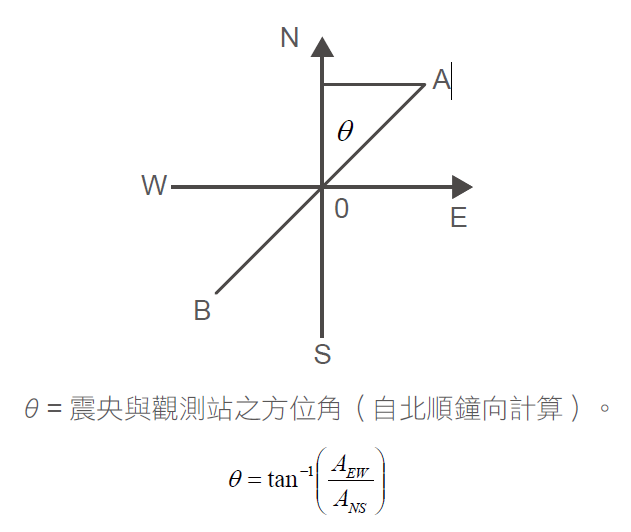
如地震站記錄到某一地震之震波，其初動方向及大小均能計算，則按向量合成法可求出震央：
A_EW = Ｐ波初動E-W分量之振幅（E為正，W為負）。
A_NS = Ｐ波初動N-S分量之振幅（N為正，S為負）。
θ = 震央與觀測站之方位角（自北順鐘向計算）。
則θ = tan^-1(A_EW/A_NS)
如圖，若初動垂直分量為上動，則震央在OB或其向B方向之延長線上；如垂直分量為下動，則震央在OA或其向A方向之延長線上。至於震央與觀測站之距離，可由下法之△求得。但因地震發生時其初動往往不明顯，故僅以單站決定震央者甚少使用。

(2)簡易多站定位法（以3站為例）

設地震波之傳播速度為常數，V_P為Ｐ波波速，V_S為Ｓ波波速，T₀ 為地震發震時間，△為測站與震央之距離，則
T_P - T₀ = △ / V_P（T_P＝Ｐ波到達時間） --------(1)
T_S - T₀ = △ / V_S （T_S＝Ｓ波到達時間）--------(2)
由(1)，(2)兩式得　T_S - T_P = △（1/V_S - 1/V_P）
∴　△ = (T_S - T_P) / ((1/V_S) - (1/V_P))
及T₀ = (T_PV_P - T_SV_S) /(V_P - V_S)
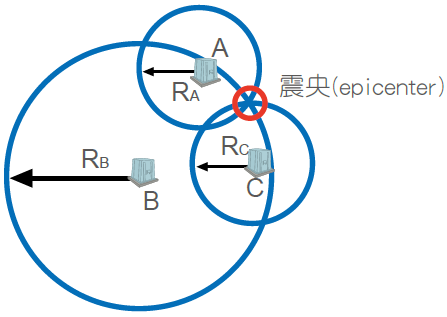
若有3站與震央之距離已知，則分別由其距離為半徑作圓，所得之交點即為震央（如圖）。

(3)多站定位法:

綜合各站所記錄之初達波的時間，利用最小平方法計算地震發生的 時間、位置及深度。

       以上之計算係假設地震波之傳播速度為常數，實際上震波傳遞波速會隨著地質構造與岩層密度等條件而不同，一般而言地震波速會隨著地層深度而增加，且水平方向也會有側向速度變化。因此實務上地震觀測必須仰賴電腦數值運算，將各地震站觀測到之P波到時、S波到時、震波頻率、最大振幅等資訊，導入預先建立之速度模型（層狀或三維模型），即可演算出發震時間、地震位置、震源深度、規模大小等震央資訊。